Better performance
We redid the backend interface to the BGL routines. This optimization gave a considerable performance increase.
test_benchmark on MatlabBGL 2.1
2008-10-07, Version 2.1, Matlab 2007b, boost 1.33.0, g++-3.4 (lib), gcc-? (mex)
airfoil west cs-stan minneso tapir large 0.223 s 0.024 s 0.390 s 0.073 s 0.046 s med NaN s 0.955 s NaN s NaN s 6.621 s small NaN s 0.758 s NaN s NaN s NaN s
test_benchmark on MatlabBGL 3.0
2008-10-07: Version 3.0, Matlab 2007b, boost 1.34.1, g++-4.0 (lib), gcc-? (mex)
airfoil west cs-stan minneso tapir large 0.183 s 0.017 s 0.222 s 0.048 s 0.037 s med NaN s 0.593 s NaN s NaN s 3.901 s small NaN s 0.543 s NaN s NaN s NaN s
Graph construction functions
MatlabBGL 2.1 had a few graph construction functions. MatlabBGL 3.0 adds the grid_graph function for line, grid, cube, and hyper-cube graphs
[G xy] = grid_graph(6,5); gplot(G,xy,'.-');
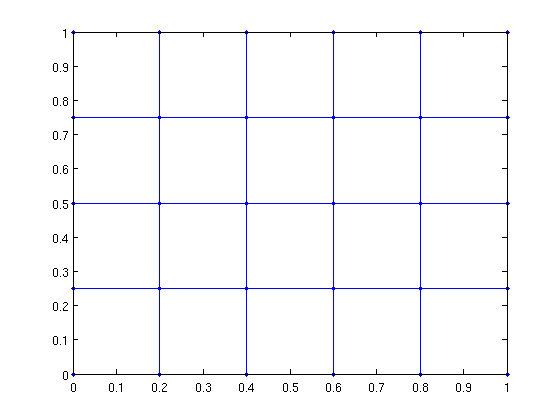
In more dimensions...
[G xyz] = grid_graph(6,5,3); G = grid_graph(2,2,2,2); G = grid_graph([3,3,3,3,3]);
Targeted search
The graph search algorithms now let you specify a target vertex that will stop the search early if possible.
A = grid_graph(50,50);
tic; d = bfs(A,1,struct()); toc
tic; d = bfs(A,1,struct('target',2)); toc
Elapsed time is 0.001580 seconds. Elapsed time is 0.000671 seconds.
Also implemented for astar_search, shortest_paths, and dfs.
Edge weights
In Matlab, there is no way to create a sparse matrix with a structural non-zero (used for MatlabBGL edges) and a value of 0 (used for MatlabBGL weights). Consequently, it's impossible to run algorithms on graphs where the edge weights are 0.
Consequently, some algorithms now take an 'edge_weight' parameter that allows you to provide a different set of edge weights which allow structural non-zeros and 0 values.
This behavior is a bit complicated, so see the REWEIGHTED_GRAPHS example for more information.
Matching algorithms
While maximum cardinality bipartite matching is just a call to max-flow, general graph matching algorithms are not. MatlabBGL 3.0 contains the matching algorithms in Boost 1.34.0.
load('../graphs/matching_example.mat'); m = matching(A); sum(m>0)/2 % matching cardinality should be 8
ans =
8
New graph statistics
We added a few new statistics functions.
Test for a topological ordering of a graph (only applies to DAGs or directed acyclic graphs)
n = 10; A = sparse(1:n-1, 2:n, 1, n, n); % construct a simple dag p = topological_order(A); test_dag(A) test_dag(cycle_graph(6)) % a cycle is not acyclic!
ans =
1
ans =
0
Core numbers can help identify important regions in a graph. MatlabBGL includes weighted and directed core numbers. Also, the algorithms return the removal time of a particular vertex, which gives interesting graph orderings.
% See EXAMPLES/CORE_NUMBERS_EXAMPLE
New algorithms for clustering_coefficients on weighted and directed graphs.
A = clique_graph(6) - cycle_graph(6); % A is a clique - a directed cycle ccfs = clustering_coefficients(A) B = sprand(A); ccfs = clustering_coefficients(B) C = A|A'; % now it's a full clique again ccfs = clustering_coefficients(C)
ccfs =
0.7600
0.7600
0.7600
0.7600
0.7600
0.7600
ccfs =
0.3480
0.4104
0.4025
0.4191
0.4156
0.4380
ccfs =
1
1
1
1
1
1
Max-flow algorithms
Since Boost added the Kolmogorov max-flow function, we added the full collection of flow algorithms to MatlabBGL.
load('../graphs/max_flow_example.mat'); push_relabel_max_flow(A,1,8) kolmogorov_max_flow(A,1,8) edmunds_karp_max_flow(A,1,8) max_flow(A,1,8,struct('algname','push_relabel')); max_flow(A,1,8,struct('algname','kolmogorov')); max_flow(A,1,8,struct('algname','edmunds_karp'));
ans =
4
ans =
4
ans =
4
Dominator tree
Dominator trees are relations about presidence in certain types of graphs. These are also called flow-graphs.
load('../graphs/dominator_tree_example.mat');
p = lengauer_tarjan_dominator_tree(A,1);
New utility functions
MatlabBGL 3.0 introduces some new utility functions.
The output of a shortest path algorithm is a predecessor matrix. To convert these predecessor relationships to a path, use the path_from_pred function.
[A xy] = grid_graph(6,5); n= size(A,1); [d dt pred] = bfs(A,1); % path = path_from_pred(pred,n) % sequence of vertices to upper corner
path =
1 2 3 4 5 6 12 18 24 30
Let's draw the path
gplot(A,xy,'r.-'); [px,py]=gplot(sparse(path(1:end-1),path(2:end),1,n,n),xy,'-'); hold on; plot(px,py,'-','LineWidth',2); hold off;
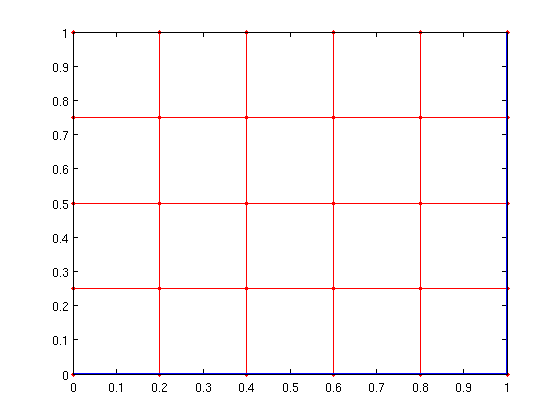
We can also create a full shortest path tree using the tree_from_pred function.
T = tree_from_pred(pred); gplot(A,xy,'r.-'); [px,py]=gplot(T,xy,'-'); hold on; plot(px,py,'-','LineWidth',2); hold off;
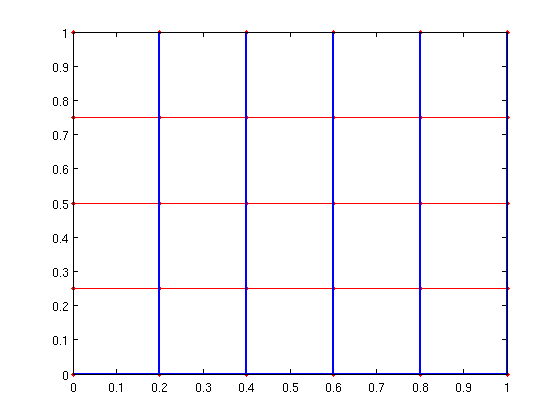
Finally, there are a few new routines to make working with reweighted graphs easier. See EXAMPLES/REWEIGHTED_GRAPHS for information about the INDEXED_SPARSE and EDGE_WEIGHT_INDEX functions.